MÁS SOBRE EL ALGORITMO

Recibimos el siguiente mensaje sobre el algoritmo en el IFE que propició el fraude:

Creia que no seria oportuno enviarte el siguiente programa de simulacion pero al leer el articulo "Guionistas del Algoritmo", quiero que quede claro que no es fantasia sino una realidad. Habemos gente que nos dedicamos a indentificar modelos dinamicos y a simularlos para predecir su comportamiento o para manejar su comportamiento en "beneficio" de ciertos objetivos. Por ejemplo en salud. Yo trabajo con celulas pero la matematica es universal y estos programas pueden ser usados en los programas de computo electoral, como se ilustra en el archivo.
Cualquier persona interesada en matematicas y programacion puede corroborarlo.
A defender el voto!

EL ALGORITMO (Ilustracion)

Considerando un sistema lineal unidimensional:
y(t) = Cx(t) + constante [funcion base]
x (t +1) = A(t)x(t), x(0) = x0 [funcion 1]

Donde:
y(t) = Cx(t) es la funcion de entrada-salida (input – output). Es aquella de la cual ya conocemos los datos de entrada y salida a diferentes tiempos o, en nuestro caso, a diferentes cantidades totales de votos.
Esta funcion podria representar los votos que obtuvo Calderon hasta antes de que la tendencia en el computo del PREP cambiara.
Asi se podia establecer los parametros optimos (A y C) para predecir con certeza la votacion por Calderon. Esto ya lo han hecho varios lectores del blog. Para asegurar un modelo exitoso para Calderon al principio del conteo del PREP tomaron distritos que asegurarian ventaja para el PAN y predeterminar su triunfo. Aunque seguramente en el PREP podrian tener una idea concreta de ese comportamiento por simulaciones anteriores.

EL OBSERVADOR: AMLO
Ahora habria que adaptar una segunda funcion. Esta representaria los votos por AMLO.
Para eso se puede construir una funcion conocida como “observador”. La cual seguira siempre asintoticamente a la funcion predeterminada (funcion 1, votos por Calderon) en base a la funcion conocida (funcion base, votos por Calderon en distritos con ventaja). El observador nunca llegara a igualarla aunque la diferencia sea infinitesimal y solo sera eso, un observador. Es importante establecer la estabilidad del observador, es decir el rango en que puede variar con respecto a la funcion base. Es decir, que tan cerca podrian llegar a quedar los votos de Obrador con respecto a los votos de Calderon. De tal manera la formula para el observador sera:
x’ (t+1) = Ax(t) + k [y(t) – C x’(t)], x’(0) = x’o
Donde k es el parametro que hace al observador estable con respecto a la funcion base.
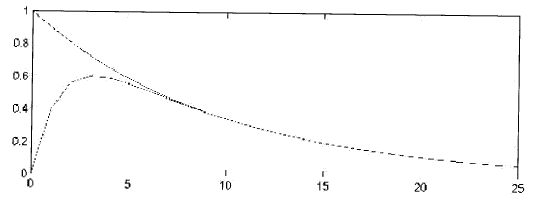
Por ejemplo /A-kC/<1 (1 puede ser cualquier unidad discrecinal de tiempo, 1 segundo, o en una eleccion 100 000 votos etc.) De tal manera: Se puede aplicar el siguiente programa y simular en un software llamado Matlab: T=25; #(estos es la cantidad de puntos (tiempos o cantidades de votacion total) de chequeo, fijado por el programista) x=zeros(1,T); xhat=zeros(1,T); #xhat representa al observador (en nuestro caso votos por Obrador) time=zeros(1,T); x(1,1)=1; xhat(1,1)=0; time(1,1)=0; A=0.9, C=0.2; # (estos son los coeficientes a establecer, solo como ejemplo elegi estos valores) for t=0:T-1 time(1,t+2)=t+1 x(1,t+2)=a*x(1,t+1); xhat(1,t+2)=2*c*x(1,t+1)+(a-2*c)*xhat(1,t+1); # elegi 2 como valor para = K*c*x... end subplot(2,1,1), plot(time,x) hold on plot(time,xhat); Si se simula este programa en el paquete MatLab se obtiene en los graficos (plots) pares de lineas que se aproximan asintoticametne pero nunca se tocan. Jugando con los coeficientes A y C, y variando los valores del parametro k se puede obtener una grafica muy similar a la del PREP.

Esta es la grafica que arroja el progama anterior. Como se observa la linea superior inicia en 1 (eso podria ser la ventaja inicial de Calderon) con respecto a la linea inferior (que representa al obervador) o a la votacion de AMLO que luego de 25 evaluaciones (ver eje horizontal) nunca llega a tocar a la funcion predeterminada (linea superior o votacion por Calderon). En este grafico la diferencia es tan minima que a simple ojo parece que se interceptan, pero en ralidad no es asi (zoom out). Esto depende del coeficiente k, arbitrariamente asignado al programa de MatLab (en el renglon 12 del programa se puede modificar el valor asignado (2) por cualquier otro). Los valores de los coeficientes A y C se pueden elegir de tal forma que las funciones (lineas) en lugar de caer crezcan, como es el caso de las votaciones con respecto a los votos totales (las cantidades se incrementa).

Cualquier estudiante de matematicas puede jugar con esto y obtener un modelo muy similar al del PREP.

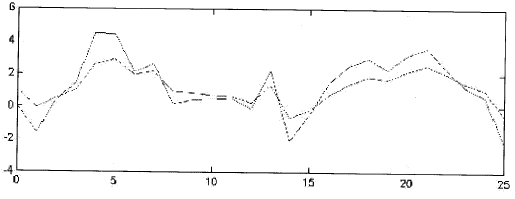
En un evento aleatorio las funciones no pueden estar tan definidas como fue el caso del PREP o la ilustracion de arriba. Generalmente muestran graficas con variaciones como se muestra abajo (tambien modelada por mi). Esta es una grafica con “ruido” y que en caso de estar integrada a un sistema es mas dificil de detectar porque tiene un comportamiento “natural”. Imaginen los graficos de las encuestadoras.